IonMonkey/LIR
LIR
Overview
IonMonkey's LIR (Low-level IR) is an SSA IR. IR nodes are represented as objects, and organized into basic blocks, which comprise a control-flow graph. Unlike MIR, LIR focuses on code generation, having a few major differences:
- It is augmented on a per-platform basis. There are shared LIR nodes that are expected to work on every platform, but platforms can also introduce their own LIR only available for a certain CPU.
- It is lightweight. LIR does not maintain def/use chains and maintains little state beyond its register allocation policies.
- Its inputs and outputs are virtual registers, rather than SSA names.
Nodes
Found in: ion/IonLIR.*, ion/LOpcodes.h, ion/LIR-$(ARCH).h, ion/LOpcodes-$(ARCH).tbl
LIR nodes are encapsulated in LInstructions, which are attached to LBlocks. LBlocks have a 1:1 mapping, and the same ordering as, MBasicBlocks, mirrored the LGraph data structure.
LInstructions have the following properties:
- An opcode identifier.
- A snapshot, containing LAllocation policies capturing the virtual registers of each SSA name on the stack at the last resume point.
- Defs: Zero or more LDefinition policies specifying the outputs of the instruction.
- Operands: Zero or more LAllocation policies specifying the inputs of the instruction.
- Temps: Zero or more LDefinition policies specifying temporary registers needed by the instruction.
To make accessing and allocating nodes as fast as possible, LInstructionHelper<D, I, T> is a template class where D is the number of definitions, I is the number of input operands, and T is the number of temporaries. Instructions should inherit from this class if possible.
Representing Values
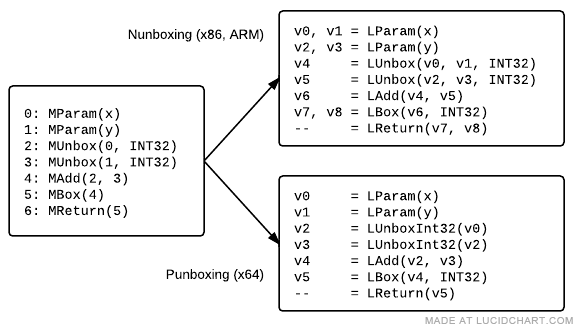
One tricky aspect of LIR is that we would like to abstract it as much as possible, however, the representation of a js::Value is architecture-specific. For instructions that define values, or take in values as operands, we use a BOX_PIECES macro which is 1 for punboxing and 2 for nunboxing.
We treat value inputs and definitions as untyped, and therefore, they are always non-constant.
Allocations
After register allocation, an instructon's Defs, Operands, and Temps are filled in with registers or stack slots. During code generation, these assignments are used to implement the instruction. For example, on x86, an LAddI (add integers) might look like:
class LAddI : public LInstructionHelper<1, 2, 0>
{
public:
LIR_HEADER(AddI);
LAddI(const LDefinition &def, const LAllocation &lhs, const LAllocation &rhs) {
setDef(0, def);
setOperand(0, lhs);
setOperand(1, rhs);
}
const LDefinition *output() {
return getDef(0);
}
const LDefinition *lhs() {
return getOperand(1);
}
const LDefinition *rhs() {
return getOperand(1);
}
};
To generate code for an LAddI, on x86, we might have something like:
void Generate(MacroAssembler &masm, LAddI *lir) {
masm.addl(ToOperand(lir->rhs()), ToRegister(lir->output()));
}
On ARM, with a three-register form, we might have something like:
void Generate(MacroAssembler &masm, LAddI *lir) {
masm.add(ToRegister(lir->lhs()), ToRegister(lir->rhs()), ToRegister(lir->output()));
}
This is possible with one data structure, because of the policies attached to operands and definitions. While the structure of an LAddI always looks the same, different architectures may specify different register allocation schemes. This is explained below.
Virtual Registers and Policies
LIR describes how the register allocator should assign physical registers or memory locations to its instructions. The heart of representing physical or virtual allocations is an LAllocation, which derives into the following classes:
- LUse, containing a virtual register and a physical allocation policy. A virtual register is an integer, and they are allocated sequentially.
- LGeneralReg, containing a general-purpose register.
- LFloatReg, containing a floating-point register.
- LArgument, containing a reference to one of the method's input arguments.
- LConstant*, a constant value.
- LStackSlot, containing a reference to a stack slot.
An LDefinition is a separate structure, a tuple containing the following properties:
- A virtual register. Every LDefinition defines a unique virtual register.
- A type (double, integer, pointer, box, etcetera).
- An LAllocation, which is the initial allocation for the definition.
Inputs
Inputs to an instruction are represented with LAllocations, and fall into the following categories:
- LUse: A use of a virtual register, with an associated policy.
- LConstant*: A constant value that will be ignored by the register allocator.
The register allocator transforms LUses into register or memory variants of LAllocation. The associated policies for doing so are:
- ANY: The instruction supports this operand being in a stack slot or register.
- REGISTER: The instruction requires this operand to be in a register.
- FIXED: Not only does this instruction require a register, it requires a specific register which is specified in the LUse.
- KEEPALIVE: Same as ANY; however, the register allocator should not apply heuristics. If the value is already in a stack slot, it should not be loaded into a register. This is used only for snapshots.
- COPY: This instruction requires the input be in a writable register. This means the register allocator will copy the input into a new register, unless it knows the value is dead.
Outputs
Outputs to an instruction are represented with LDefinitions. As mentioned earlier, they define unique virtual registers. LDefinitions have the following policies:
- DEFAULT, meaning a register.
- PRESET, meaning the register allocator must use the allocation specified in the definition's LAllocation.
- MUST_REUSE_INPUT, which requires that the definition have the same register as the 0th input operand. This is for two-register architectures like x86, and is conceptually similar to the COPY input policy.
- REDEFINED, which says that this LDefinition is actually the same as another LDefinition. When REDEFINED is used, the LDefinition is completely ignored. The instruction is informing the register allocator that, rather than producing a new output, it is a "pass-through" mechanism (like boxes and unboxes on x86).
If the LDefinition does not have a PRESET or REDEFINED policy, its LAllocation is filled in during register allocation.and are effectively removed during register allocation.
Lowering
Class Hierarchy
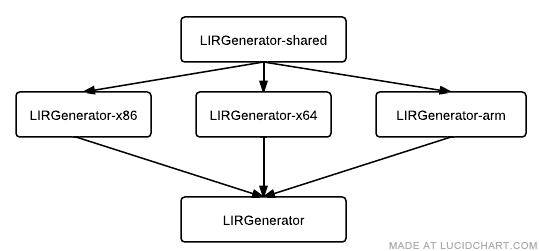
The process of converting MIR to LIR is Lowering. Lowering is implemented by LIRGenerator, which defines functions to lower each MIR instruction. To maximize the amount of code we can share between all platforms, LIRGenerator has a somewhat roundabout class hierarchy:
The base class, LIRGeneratorShared, contains basic functionality that is used by derived classes. LIRGenerator$(ARCH) implements architecture-specific lowering. Finally, LIRGenerator derives from exactly one of the architecture-specific base classes, depending on the platform.
We try to move as much logic into the derived-most LIRGenerator as possible. For example, math operations almost always have a conceptual three-register form (two inputs and an output), but on x86 generate two-register form code. Rather than exposing these differences in the structure of LIR, we expose them in allocation policies, and thus math-oriented policies are simply exposed on a per-architecture basis.
Process
LIR is generated by iterating over MIR in reverse-postorder. Mapping from MIR to LIR is basically 1:1. When lowering an instruction, we first create LAllocations for its inputs. Depending on what the architecture allows, an operand begins as either a virtual register or a constant. Virtual registers are allocated when defining LIR definitions, and also attached to corresponding MIR nodes for later uses.
If a LIR instruction defines a Value, and values are two definitions (as is the case on nunboxing platforms), then two virtual registers are allocated. However, only the first is associated with its corresponding MIR node - we assume virtual registers are contiguous and thus the distance between two virtual registers defining one Value is 1.
Below is an example of how MIR might lower on x86 versus x64:
Emitting at Uses
If some value has trivial rematerialization, for example, emitting an integer constant, or a box on x86, we can elect to emit the instruction at each point it is used, rather than when it is defined. The facility for doing this is to call emitAtUses() on the MIR being lowered. This informs the LIRGenerator to defer lowering.
Later, if another instruction actually requires a virtual register for an input that has yet to be lowered, it will attempt to immediately lower that input. The visitor can check isEmittedAtUses on the instruction to see whether it must actually create LIR.
Phis
Phis in LIR define exactly one virtual register, and have an input virtual register for each predecessor block. On nunboxing platforms, an untyped (boxed) phi produces two LIR phi nodes: one for the type, and another for the payload. Phis are ignored during code generation, as register allocation breaks SSA form.